DP(Dynamic Programming,动态规划)也是强化学习的重要基础,因为MDP的天然属性,使得DP能够应用到RL上,这章里的策略评估、策略迭代、值迭代都用到了DP。
DP(Dynamic Programming)
本章主要使用一个例子来说明相关的概念,如下图
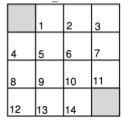
- 所有的奖励都为 -1,也就是 $R_{ss’}^a$ 恒等于 -1
- 中间状态5、6、9、10有四个动作(向上、向下、向左、向右),靠边状态1、2、4、8、13、14、7、11有三个动作(不能出格子),靠角落的状态3、12有两个动作,阴影状态为结束状态
- $\gamma = 1$
- 初始策略为均匀随机策略
简介
动态规划的基本概念,相信学过数据结构与算法的都知道,这里简单介绍一下。它是一种用来解决复杂问题的方法,将问题分解为若干个子问题。它需要问题满足下面几个属性:
- 最优子结构
- 重叠子问题
而马尔科夫决策过程正好符合这两个属性。
马尔科夫决策过程中的动态规划假设,已知MDP的所有属性,来进行规划。
-
对于预测问题来说
- 输入:MDP $<S,A,P,R,\gamma>$ 和 策略 $\pi$
- 输出:该策略的值函数 $v_\pi$
-
对于控制问题来说
- 输入:MDP $<S,A,P,R,\gamma>$ 和 初始策略 $\pi$
- 输出:最优的值函数 $v_\ast$ 和最优的策略 $\pi_\ast$
策略评估(Policy Evaluation)
问题:评估一个给定的策略 $\pi$
解决方案:通过不断对贝尔曼期望方程的备份进行迭代完成
步骤:
- 在每一轮迭代 k + 1
- 对所有的状态 $s \in S$
- 从 $v_k(s’)$ 更新 $v_{k + 1}(s)$
- 这里 $s’$ 是状态 $s$ 的后继状态
通过图示来展示更新公式

对于这个网格例子中,我们对随机策略 $\pi$ 进行策略评估,我们只看左半部分,先不看右半部分

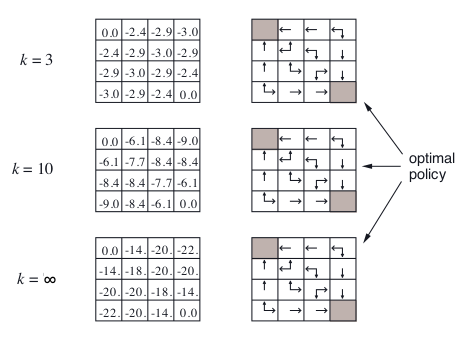
希望你能亲自计算一下,看自己计算的是否和图示吻合,这里举个例子,对于第一行第二列的格子,值函数记为 $v$
- $k = 0, v = 0$
- $k = 1, v = \frac{1}{3} \times (-1 + 0) + \frac{1}{3} \times (-1 + 0) + \frac{1}{3} \times (-1 + 0) = -1$
- $k = 2, v = \frac{1}{3} \times (-1 + 0) + \frac{1}{3} \times (-1 + -1) + \frac{1}{3} \times (-1 + -1) = -\frac{5}{3} \approx -1.7$
- $\cdots$
策略迭代(Policy Iteration)
我们知道了怎么评估一个策略,为了得到最优策略,我们怎么去提升这个策略呢?给定初始策略 $\pi$
-
评估这个策略 $\pi$
-
提升这个策略,通过贪婪的执行动作
通过迭代上面两个步骤,我们最终会得到最优策略,可能需要很多步,但最终会得到最优策略 $\pi_\ast$
下面的图示是原教程中的,是帮助理解策略迭代的
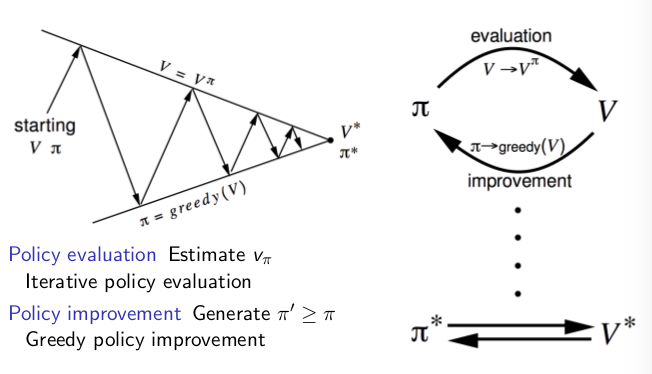
那么策略迭代真的能得到最优策略吗?下面简单的证明一下
- 考虑一个确定性策略,$a = \pi(s)$
-
我们贪婪的提升这个策略
-
通过这个贪婪的动作提升了状态 $s$ 的值函数
-
因为每一步贪婪都提升了值函数,下面我们证明 $v_{\pi ‘}(s) \ge v_\pi(s)$
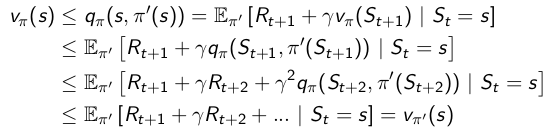
- 最终我们得到了 $v_\pi(s) = v_\ast(s),\forall{s \in S}$ ,所以最终得到的策略 $\pi$是最优策略
对于这个网格例子来说,观察上述那张图片的右半部分,是贪婪的过程,实际上按照上面的方法,我们是要等到左边的迭代评估过程收敛之后,再进行一次贪婪。但是我们左边的迭代评估其实需要很多轮,我们应该有一个停止条件,比如 值函数的$\epsilon$收敛(也就是值函数的变化很小,这个时候停止迭代评估),或者在固定的 $k$ 步后停止。而我们的图片示例中,是每进行一次迭代都贪婪一次,发现当 $k = 3$ 时,已经得到最优策略了,所以有时并不需要等到当前策略的评估迭代收敛后,再进行贪婪。
那么按照图示中,我们每迭代一次就进行一次贪婪可以吗?也就是固定的 $k = 1$,每次的评估过程只迭代一次。实际上这种方法等同于值迭代(Value Iteration),下面会讲到。
广义的策略迭代如下图所示
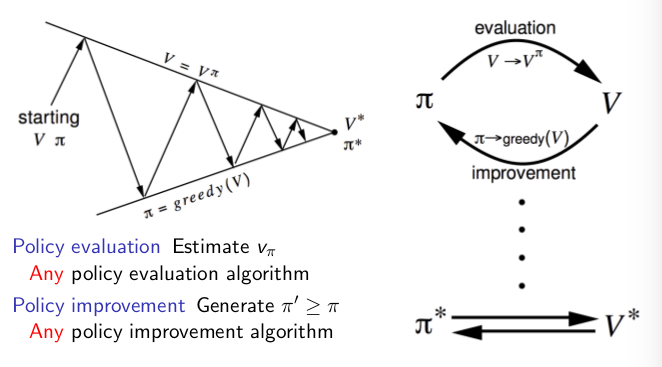
值迭代(Value Iteration)
任何一个最优策略可以分为以下两部分
- 最优动作 $a_\ast$
- 跟着一个从后继状态 $s’$开始的最优策略
一个策略 $\pi(a \mid s)$实现了从状态 $s$ 开始的最优值, $v_\pi(s) = v_\ast(s)$,当且仅当:对于从$s$可达的所有状态 $s’$ 都有 $v_\pi(s’) = v_\ast(s’)$.
所以如果我们知道了子问题的解决方案 $v_\ast(s’)$,那么
这就是值迭代的思想,直观来看,我们应该从马尔科夫链的末端开始计算。如下图,先计算叶子节点,再计算内部节点
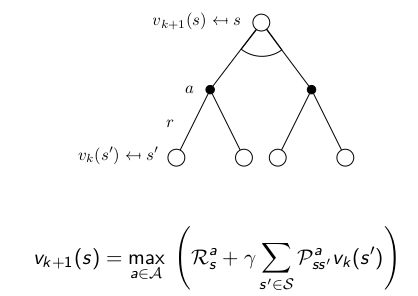
这里举个例子,不同于开始的例子,这里只有一个终止状态
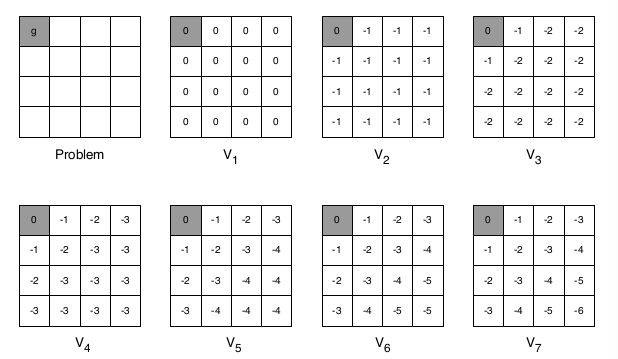
这个例子中,从末端开始计算,也就是阴影终止状态开始计算,第一轮初始化为0,第二轮计算位置(1,1),第三轮计算位置(1,2)、(2,1),第四轮计算位置(1,3)、(2,2)、(3,1),…
这里结合上章的知识总结一下:
| 问题 | 贝尔曼方程 | 算法 |
|---|---|---|
| 预测问题 | 贝尔曼期望方程 | 迭代策略评估 |
| 控制问题 | 贝尔曼方程 + 贪婪策略提升 | 策略迭代 |
| 控制问题 | 贝尔曼最优方程 | 值迭代 |
后面还有异步的动态规划和值函数收敛的证明,这里省略,有兴趣的朋友请参考原ppt.