MDP(Markov Decision Process,马尔科夫决策过程)是强化学习的重要基础,所有的强化学习问题都可以抽象成一个MDP。在原教程中,这章的讲解思路是从简单到复杂一步一步讲解的,从MP(Markov Process,马尔科夫过程)到MRP(Markov Reward Process,马尔科夫奖励过程)再到MDP(Markov Decision Procee,马尔科夫决策过程)。我这里是直接讲解MDP,主要是我觉得没有必要讲解MP和MRP,因为这是为了讲解清楚MDP而引入的中间产物,后面不会用到。我尽量讲清楚,如果您觉得哪里不太清楚的,欢迎讨论,或者观看原视频和ppt。
MDP(Markov Decision Process)
这里引入一个例子来讲解MDP相关概念。这个例子是原教程中的一个例子,描述的是一个学生的MDP。圆圈表示的是状态,方块表示终止状态。箭头表示状态转移,箭头上的小数表示转移概率,箭头上的文字表示动作,比如Facebook表示刷Facebook的动作,Sleep表示睡觉的动作。这个例子还是挺符合生活的,比如如果学生刷Facebook,他有90%的概率继续刷Facebook。采用的原教程中的截图,因为一张图表达不了所有的信息,所以这里建议两张图结合着看。至于第一张图比第二张图少一个状态,这个无所谓,不妨碍后面相关概念的理解。
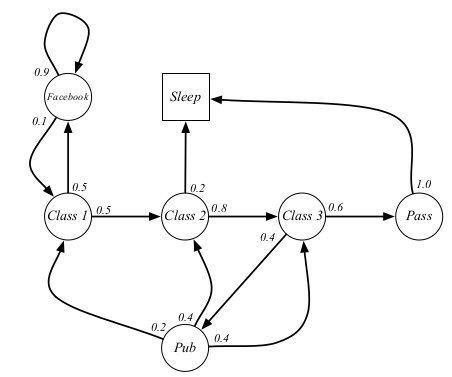
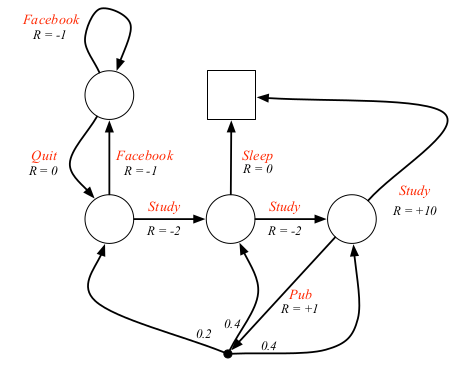
马尔科夫决策过程正式的定义了强化学习中的环境,这里的环境是可完全观测的。几乎所有的强化学习问题都可以形式化为MDP,例如
- 最优控制主要处理连续MDP
- 不可完全观测的问题可以转化成MDP
- Bandits可以看做是只有一个状态的MDP
马尔科夫的形式化定义为,一个五元组 $<S,A,P,R,\gamma>$
- $S$ 是一个有限的状态集合
- $A$ 是一个有限的行为集合
- $P$ 是一个状态转移概率矩阵
- $R$ 是一个奖励函数
- $\gamma$ 是一个折扣因子 $\gamma \in [0,1]$
马尔科夫属性(Markov Property)
未来的状态只取决于当前的状态,与过去的状态无关。
A state $S_t$ is Markov if and only if
- 前面说过状态是历史的函数,所以状态里捕捉了历史中的所有相关信息
- 一旦知道一个状态,历史信息可以丢掉
状态转移矩阵
对于状态 $s$ 和后继状态 $s’$ ,状态转移概率为
状态转移矩阵 $P$ 为
其中,矩阵中所有元素的和为1。
比如学生MDP例子中的状态转移概率矩阵为

回报(Return)
回报 $G_t$ 指的是t步的折扣奖励和
- 对于未来的奖励有一个折扣因子 $\gamma$ ,$k + 1$步之后的奖励 $R$ 计为 $\gamma^k R$
- 折扣因子的取值决定了我们如何看待未来奖励
- $\gamma$ 靠近0表示只看不重视未来奖励,目光短浅
- $\gamma$ 接近1表示重视未来奖励,目光长远
那么,为什么要有折扣因子呢?
- 数学上的便利,比如收敛等等
- 避免无限的回报在循环的马尔科夫链中,影响评估
- 对未来奖励的不确定性
- 联想到金融,现在的钱比未来的钱更有价值
- 人类的认知更偏向于即时奖励
有时可能使用无折扣的奖励,如果所有的序列都可以终止。
对于学生MDP的例子来说,我们通过采样一些序列来展示回报怎么算,假设 $S_1 = C1, \gamma = \frac{1}{2}$,随机采样的一些序列可能是
- C1 C2 C3 Pass Sleep
- C1 FB FB C1 C2 Sleep
- C1 C2 C3 Pub C2 C3 Pass Sleep
- C1 FB FB C1 C2 C3 Pub C1 FB FB FB C1 C2 C3 Pub C2 Sleep
回报如下
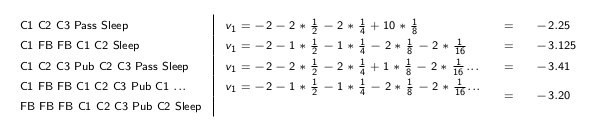
这是教程中的截图,个人认为这里的 $v1$ 改为 $G1$ 较好。
值函数
状态值函数 $v_\pi(s)$ 给出了按照策略 $\pi$ 状态 $s$ 的长期价值。状态值函数定义为按照策略 $\pi$ 从状态 $s$ 开始的期望回报。
对于学生MDP的例子来说,如果我们已知环境,是可以算出状态值函数的,关于具体怎么算,后面会讲。这里先只是展示一下不同 $\gamma$ 的状态值函数具体值。
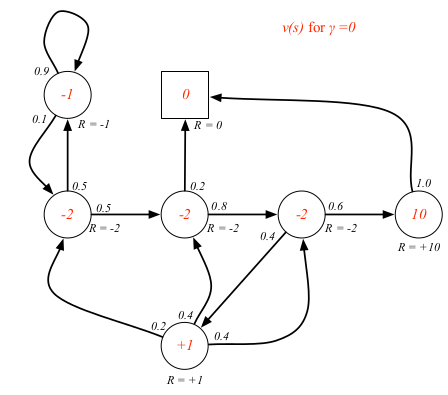

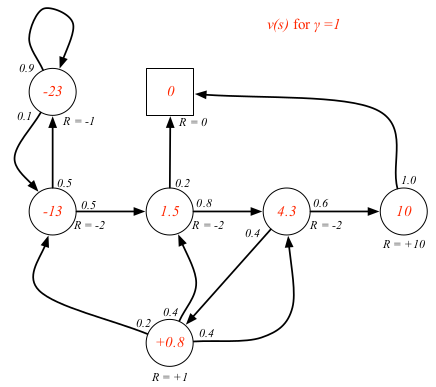
状态-动作值函数 $q_\pi(s,a)$ 指的是按照策略 $\pi$ ,从状态 $s$ 开始执行动作 $a$ 的长期价值。状态-动作值函数定义为按照策略 $\pi$ 从状态 $s$ 开始执行动作 $a$ 的期望回报。
贝尔曼期望方程
状态值函数可以分解成两部分:
- 即时奖励 $R_{t + 1}$
- 后继状态的折扣价值 $\gamma v_\pi(S_{t + 1})$
同理,状态-动作值函数也可以分解成两部分:
- 即使奖励 $R_{t + 1}$
- 后继状态 $S_{t+1 }$ 和动作 $A_{t+1}$ 的折扣价值 $q_\pi(S_{t+1}, A_{t+1})$
我们尝试去掉期望,改成概率形式,同时表明 $v_\pi$ 和 $q_\pi$ 之间的微妙关系。(建议看懂下面四个式子,弄透彻)
| 图示 | 公式 |
|---|---|
 |
|
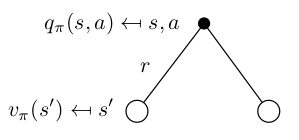 |
|
 |
|
 |
对于学生MDP的例子来说,我们展示上述第三个公式的一个例子,其中 $\gamma = 1$
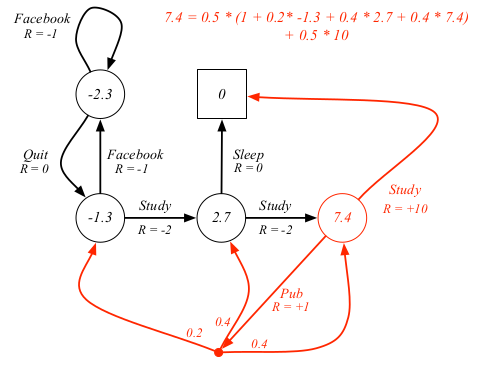
如果用矩阵形式,贝尔曼期望方程可以简单的写作
同时,如果环境(现在说到环境,就应该有条件反射,指状态转移矩阵和奖励函数)已知,那么有直接的闭式解
但是这种方法只适合与状态空间小的MDP,对于规模大的MPD,有一些迭代的方法来解决,比如
- 动态规划
- 蒙特卡洛(Monte-Carlo)评估
- TD(Temporal-Difference)学习
最优值函数和最优策略
最优状态值指的是所有的策略中得到的最大状态值,最优状态-动作值指的是所有的策略中得到的最大状态-动作值。
最优值函数表明了MDP可能的最好性能,当我们知道最优值函数,这个MDP问题就得到解决了。
对于学生MDP的例子来说,最优值函数和最优状态-动作值函数如下
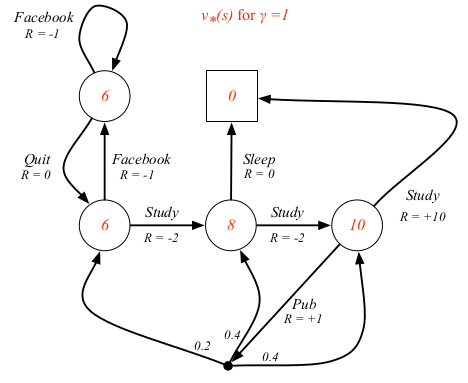
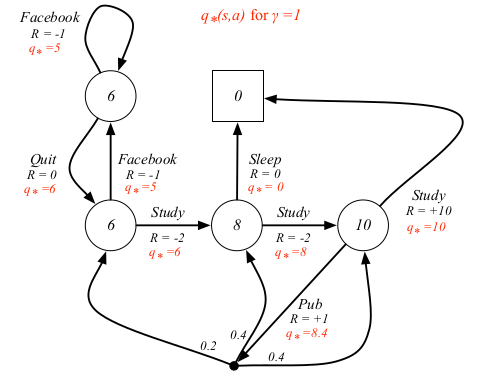
最优策略指的就是取得最优值函数时所依照的策略。
我们定义一个策略偏序
$\pi \ge \pi’$ if $v_\pi(s) \ge v_\pi’(s), \forall{s}$
对于所有的MDP
- 一定存在一个最优策略 $\pi_\ast$ 优于其他的策略, $\pi_\ast \ge \pi, \forall{\pi}$
- 按照最优策略一定得到最优状态值函数,$v_{\pi_\ast}(s) = v_\ast(s)$
- 按照最优策略一定得到最优状态-动作值函数,$q_{\pi_\ast}(s,a) = q_\ast(s,a)$
那么如何求最优策略呢?
一个最优策略可以通过最大化 $q_\ast(s, a)$得到
- 对于任何一个MDP,一定存在一个确定性的最优策略
- 如果我们知道最优状态-动作值函数 $q_\ast(s,a)$,相当于得到了最优策略
对于学生MDP的例子来说,最优策略用红线标出
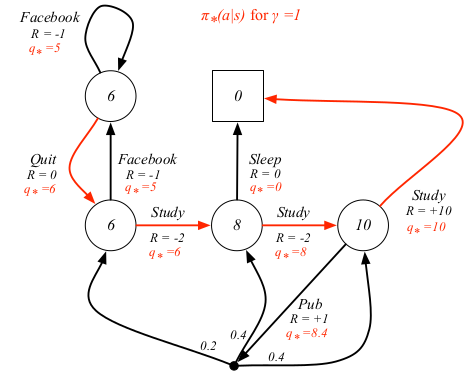
贝尔曼最优方程
这里是针对最优值函数 $v_\ast$ 和 $q_\ast$ 的贝尔曼方程,同时揭示了它们之间的关系,建议同贝尔曼期望方程结合着看
| 图示 | 公式 |
|---|---|
 |
|
 |
|
 |
|
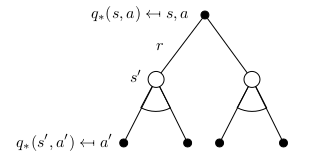 |
对于学生的MDP例子,我们展示上述第三个公式的例子
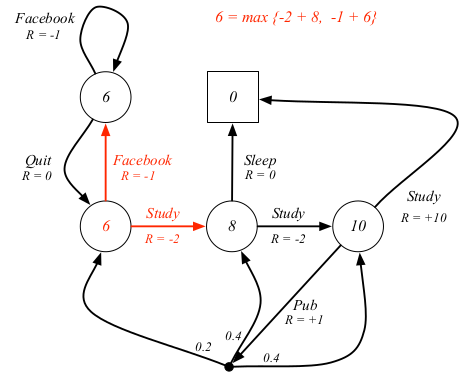
与上述的贝尔曼期望方程不同,贝尔曼最优方程是非线性的,一般来说没有闭式解,有许多迭代的解决方案,比如
- 值迭代
- 策略迭代
- Q-learning
- Sarsa